Nonlinear fusion is optimal for a wide class of multisensory tasks

New preprint! A simple way to extend the classical evidence weighting model of multimodal integration to solve a much wider range of naturalistic tasks. Spoiler: it's nonlinearity. Works for SNNs/ANNs. 🧵 with @MarcusGhosh @GabrielBna1 @BormuthVolker https://t.co/4to71pOfsd pic.twitter.com/E3ty5nlyp1
— Dan Goodman (@neuralreckoning) July 27, 2023

Think about the infamous 'cocktail party': you use synchrony between lip movements and sounds to help you hear in a noisy environment. But the classical model throws away that temporal structure, instead just linearly weighting visual and auditory evidence.
— Dan Goodman (@neuralreckoning) July 27, 2023

We call this algorithm accumulate-then-fuse because first you accumulate evidence over time within a modality, followed by linearly fusing across modalities. We propose instead to (nonlinearly) fuse-then-accumulate. This works much better with pretty much any nonlinearity. pic.twitter.com/caUnKVqNW6
— Dan Goodman (@neuralreckoning) July 27, 2023

This work started when we were training spiking neural networks with surrogate gradient descent (thanks @hisspikeness) to solve the classical multimodal task where multimodal signals are independent. To our surprise, we didn't need a multimodal area to solve this task! pic.twitter.com/1RxQ5lxG1d
— Dan Goodman (@neuralreckoning) July 27, 2023

In our comodulation tasks the evidence within a modality is forced to be balanced, and only the joint temporal structure carries information. Sure enough, we found you need a multimodal area to do this task (and in unpublished pilot data, the humans in our lab can do this task). pic.twitter.com/1eTeK1CnRc
— Dan Goodman (@neuralreckoning) July 27, 2023

But this task is kind of unrealistic so we designed a "detection task" where the signal is only on at unknown times, the rest of the time you get noise. You can do this with or without a multimodal area, but there are big differences in performance when the signal is sparse. 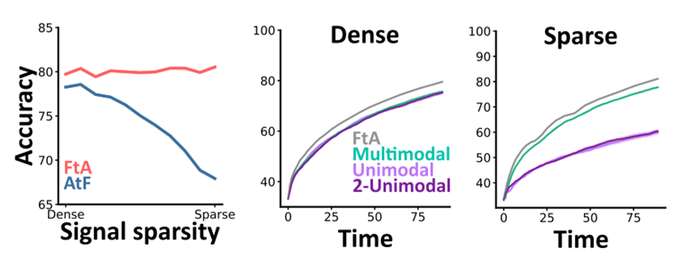pic.twitter.com/CVkzKKpjOM
— Dan Goodman (@neuralreckoning) July 27, 2023

This seems likely to be important in natural settings because fast and accurate reactions to sparse information could make all the difference in a predator-prey interaction. 🐈🐁 And the more complex the task, the bigger the performance difference.
— Dan Goodman (@neuralreckoning) July 27, 2023

The optimal nonlinearity is softplus(x)=log(1+be^cx) but training artificial neural networks with different nonlinearities like ReLU or sigmoid is just as good in practice. The solution extends to continuous observations, eg. for Gaussian noise you need softplus and quadratic.
— Dan Goodman (@neuralreckoning) July 27, 2023

Can we relate this to experimental data? One measure used is additivity: how much neurons respond to multimodal signals than you'd guess from unimodal responses. We found high additivity was more important in tasks where FtA did better than AtF, largely due to time constants. pic.twitter.com/2jtBGtAgpZ
— Dan Goodman (@neuralreckoning) July 27, 2023

Plus, we can look at behaviour. In our sparse detection task we can predict which trials subjects are likely to make mistakes on if they use AtF rather than FtA (by plotting trials based on weight of evidence assuming AtF=x or FtA=y). pic.twitter.com/6JNUEQvNms
— Dan Goodman (@neuralreckoning) July 27, 2023

We haven't done the experiments to prove this is what we do (yet), but:
⭐ It's consistent with previous experiments (as it is a generalisation of AtF)
⭐ It's the solution found when training spiking or artificial NNs
⭐ It gives better performance with few extra parameters
— Dan Goodman (@neuralreckoning) July 27, 2023

For more details check out the beautiful HTML version of the preprint on @curvenote (many thanks for the support!):https://t.co/aSclRRJQzn

or the good old PDF at @biorxivpreprint:https://t.co/4to71pOfsd

Let us know what you think!
— Dan Goodman (@neuralreckoning) July 27, 2023

Nonlinear fusion is optimal for a wide class of multisensory tasks

Ghosh M, Béna G, Bormuth V, Goodman DFM

Preprint

Abstract

Animals continuously detect information via multiple sensory channels, like vision and hearing, and integrate these signals to realise faster and more accurate decisions; a fundamental neural computation known as multisensory integration. A widespread view of this process is that multimodal neurons linearly fuse information across sensory channels. However, does linear fusion generalise beyond the classical tasks used to explore multisensory integration? Here, we develop novel multisensory tasks, which focus on the underlying statistical relationships between channels, and deploy models at three levels of abstraction: from probabilistic ideal observers to artificial and spiking neural networks. Using these models, we demonstrate that when information provided by different channels is not independent, linear fusion performs sub-optimally and even fails in extreme cases. This leads us to propose a simple nonlinear algorithm for multisensory integration which is compatible with our current knowledge of multimodal circuits, excels in naturalistic settings and is optimal for a wide class of multisensory tasks. Thus, our work emphasises the role of nonlinear fusion in multisensory integration, and provides testable hypotheses for the field to explore at multiple levels: from single neurons to behaviour.

Nonlinear fusion is optimal for a wide class of multisensory tasks

Abstract

Links

Related videos

Categories